Kristalni sustavi
U kristalima se određeni prostorni raspored atoma, iona ili molekula (čestica) periodički ponavlja u tri smjera u prostoru. Takav raspored čestica opisan je trodimenzionalnom kristalnom rešetkom, koja se definira osima kristalne rešetke (a,b,c) i kutovima među njima (α, β, γ). Najmanji dio kristala koji se periodički ponavlja u tri smjera u prostoru uzduž osi kristalne rešetke naziva se jedinična ćelija kristalne rešetke.[1]
Kristalna familija je najmanji set prostornih grupa koji za bilo koji od svojih članova sadrži sve prostorne grupe Bravaisove klase i sve prostorne grupe geometrijske kristalne klase kojoj taj član pripada.[2] Dva kristala pripadaju istoj kristalnoj familiji ako imaju isti tip kristalne rešetke, pri čemu se smiju razlikovati po centriranju atoma (Npr. monoklinska primitivna rešetka (mP) i monoklinska bazno centrirana kristalna rešetka (mS) pripadaju istoj kristalnoj familiji jer dijele isti tip kristalne rešetke, ali nisu nužno iste po centiranju atoma). U dvodimenzionalnom prostoru, sve kristalne rešetke subordinirane istoj kristalnoj familiji imaju istu simetriju. U trodimenzionalnom prostoru, pravilo vrijedi za pet kristalnih familija (triklinsku, monoklinsku, ortorompsku, tetragonsku i kubičnu), dok je kod heksagonske kristalne familije postoje dva tipa kristalnih rešetki s različitom simetrijom (heksagonska i romboedarska rešetka). Kristali s romboedarskom rešetkom pripadaju trigonskom kristalnom sustavu heksagonske kristalne familije, dok obrat nužno ne vrijedi pri čemu kristali trigonskog kristalnog sustava mogu pripadati ili romboedarskom ili heksagonskom sustavu kristalne rešetke. Kristalni sustav skup je geometrijskih kristalnih klasa prostornih grupa.[2] Geometrijska kristalna klasa klasificira simetrijske grupe vanjskog oblika kristala prema njegovom morfološkoj simetriji. U teoriji grupa, simetrijska grupa nekog objekta je skup svih simetrijskih operacija čijom primjenom na objekt taj objekt ostaje invarijantan, odnosno nepromijenjen.[3] Poštoji šest mogućih kristalnih familija i sedam kristalnih sustava kojima je moguće opisati kristalizaciju tvari.
U sljedećoj tablici su usustavljena osnovna svojstva kristalnih familija, sustava i kristalnih rešetaka u trodimenzijskom prostoru:
| Bravaisove rešetke | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Kristalna familija | Kristalni sustav | Kristalna rešetka | Geometrija kristalne rešetke | Minimalna simetrija
kristalne rešetke |
Slika jedinične ćelije
kristalne rešetke |
Primitivna (P) | Bazno-centrirana (S) | Prostorno centrirana (I) | Plošno-centrirana (F) |
| Triklinska (a) | Triklinska | a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90° |
Nema |  |
 |
||||
| Monoklinska (m) | Monoklinska | a ≠ c
α = γ = 90°, β ≠ 90° |
1 digira ili
1 zrcalna ravnina |
 |
 |
 |
|||
| Rompska (o) | Rompska | a ≠ b ≠ c
α = β = γ = 90° |
3 digire ili 1 digira i
2 zrcalne ravnine |
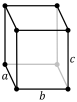 |
 |
 |
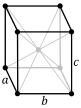 |
 | |
| Tetragonska (t) | Tetragonska | a = b ≠ c
α = β = γ = 90° |
1 tetragira | 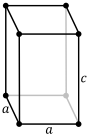 |
 |
 |
|||
| Heksagonska (h) | Trigonski | Romboedarska | a = b = c
α = β = γ ≠ 90° |
1 trigira |  |
 |
|||
| Heksagonska | a = b
α = β = 90°, γ = 120° |
1 heksagira |  |
 |
|||||
| Heksagonski | Heksagonska | ||||||||
| Kubična (c) | Kubična | a = b = c
α = β = γ = 90° |
4 trigire | 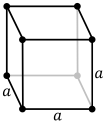 |
 |
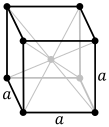 |
 | ||
- ↑ Sikirica, Korpar, Čolig: Kemija s vježbama 1, Školska knjiga, Zagreb, 2000., ISBN 953-0-20540-6, str. 152-155
- ↑ a b Hahn, Th., ur. 1. listopada 2006. International Tables for Crystallography. International Tables for Crystallography. International Union of Crystallography. Chester, England. ISBN 978-0-7923-6590-7
- ↑ Fundamental crystallography. Online Dictionary of Crystallography. Pristupljeno 5. srpnja 2021.
